Romps, The Stochastic Parcel Model: A deterministic parameterization of stochastically entraining convection, JAMES, 2016
Paper
Description
How much will the Earth warm due to the burning of coal, oil, and natural gas? Unfortunately, even if we could predict how much of these fossil fuels we are going to burn before quitting the habit, we still would not know the answer to this question. Burning fossil fuels adds CO2 to the atmosphere, but there is uncertainty as to how much warming an increase in CO2 causes. Estimates of Earth's "climate sensitivity" -- the amount of global warming for each doubling of atmospheric CO2 -- range over roughly 3 to 9 Fahrenheit. To date, we have increased CO2 concentrations by 40%, and we are likely to quadruple CO2 before halting further CO2 emissions. A quadrupling -- which is two doublings -- would lead to a global mean temperature increase in the range of 6 to 18 F, with higher warming over middle and high latitudes and over land where people live.
While even the low end of this range (6 F) would transform the planet in fundamental ways (e.g., melting ice around the world, inundating coastal cities with rising sea levels, substantially increasing the frequency of severe weather and lightning, and making hot weather all the more intolerable), the high end of this range (18 F) would be truly catastrophic. There is great urgency, therefore, to find out what exactly Earth's climate sensitivity is. To do so, however, we need to tackle the largest source of this uncertainty, which -- according to many studies -- has to do with the modeling of convective entrainment in global climate models (GCMs).
The problem is that we have not known how to represent entrainment correctly in the convective parameterizations within GCMs, and that has contributed substantially to the wide range of estimated climate sensitivities. Some evidence for how entrainment operates, and, therefore, how to represent it algorithmically in a GCM, was presented by a 2010 JAS paper, which showed that entrainment events can be described as a Poisson process. This was followed up with another 2010 JAS paper that described how to build a convective parameterization (the Stochastic Parcel Model; SPM) using this insight. Unfortunately, this implementation of the SPM was far too slow (by many orders of magnitude) to be used in a GCM.
In this paper, the SPM is reformulated to make it computationally efficient. Instead of simulating a large number of individual Lagrangian cloud parcels, each of which are subject to Poisson-process entrainment and buoyancy sorting, this new version of the SPM uses semi-analytical techniques to calculate the convective fluxes resulting from an infinite number of these cloud parcels. The resulting scheme is fast and, unlike its Lagrangian predecessor, deterministic. Comparisons with large-eddy simulations show that the SPM in a single-column model faithfully replicates the PDFs of buoyancy, vertical velocity, liquid water, ice, and other quantities.
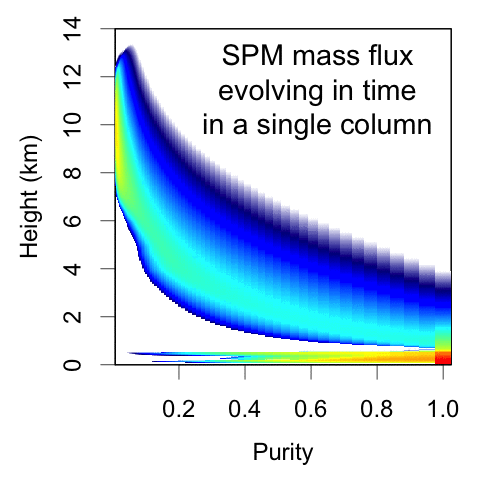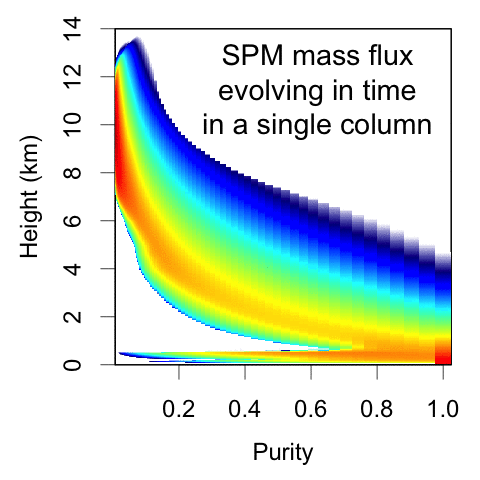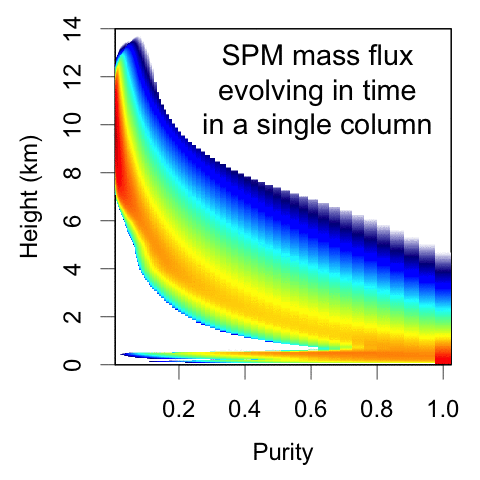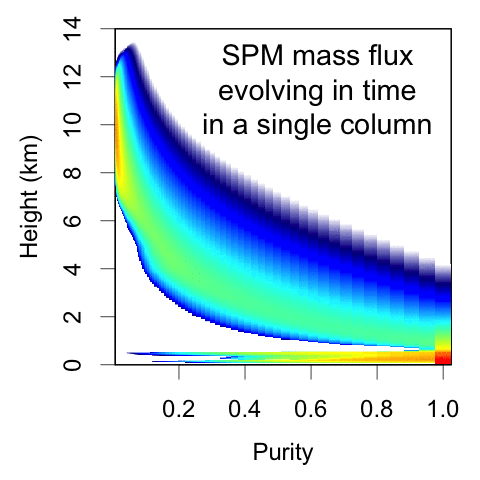
The reformulated SPM represents convective mass flux as a function of height and purity, where purity is a measure of the net entrainment experienced by the parcel. This is NOT a spectral plume model; the underlying equations are calculating how parcels move among these purity bins as they rise due to Poisson-process entrainment events.