Romps, Weak pressure gradient approximation and its analytical solutions, JAS, 2012
Paper
Description
The biggest obstacle facing numerical simulations of the atmosphere is the wide range of length scales involved. At the large end of the size spectrum, there are atmospheric circulations that extend for many thousands of kilometers. At the small end of the size spectrum, there are eddies with scales of tens of meters that are responsible for the turbulent transport into and out of clouds. One approach, taken by global climate models (GCMs), is to resolve the large scales while using a sub-grid-scale model for the small scales (i.e., a convective parameterization). Another approach is to resolve the small scales while using a supra-domain-scale model for the large scales. Using analytical solutions to the Boussinesq equations, this paper compares two types of supra-domain-scale parameterizations: the WTG (weak temperature gradient) and WPG (weak pressure gradient) approximations. The analysis suggests that the WPG scheme should be more accurate than WTG for both steady-state and transient solutions.
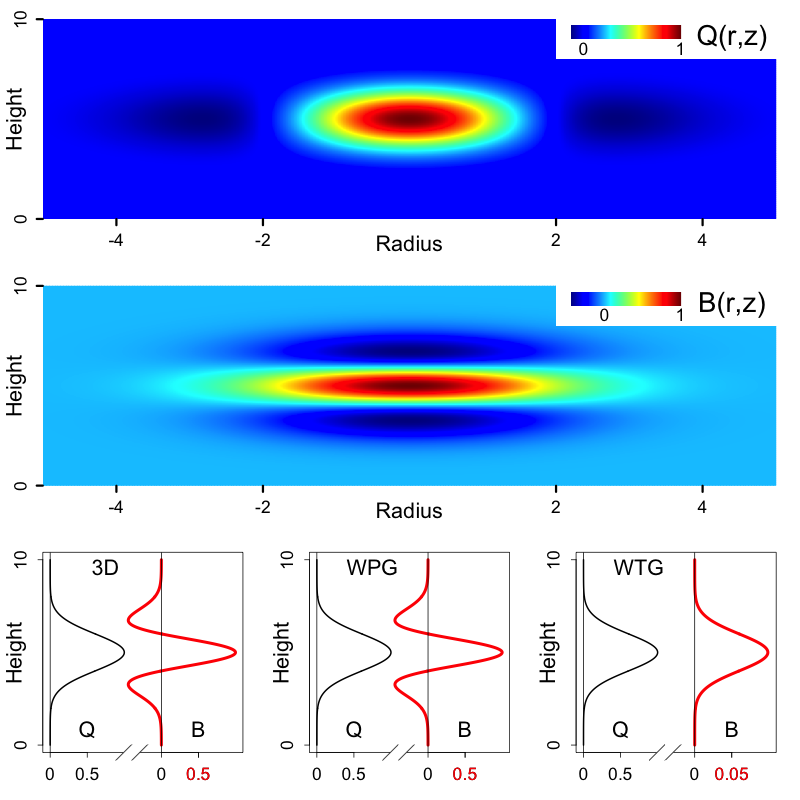
The top two panels give a cylindrically symmetric 3D steady-state solution to the Boussinesq equations; heating Q is in the top panel, and the buoyancy B is in the middle panel. The buoyancy B at r=0 is given in red in the bottom-left panel. The predictions for B given by WPG and WTG are shown in the bottom-middle and bottom-right panels, respectively.