Edman and Romps, Beyond the rigid lid: Baroclinic modes in a structured atmosphere, JAS, 2017
Paper
Description
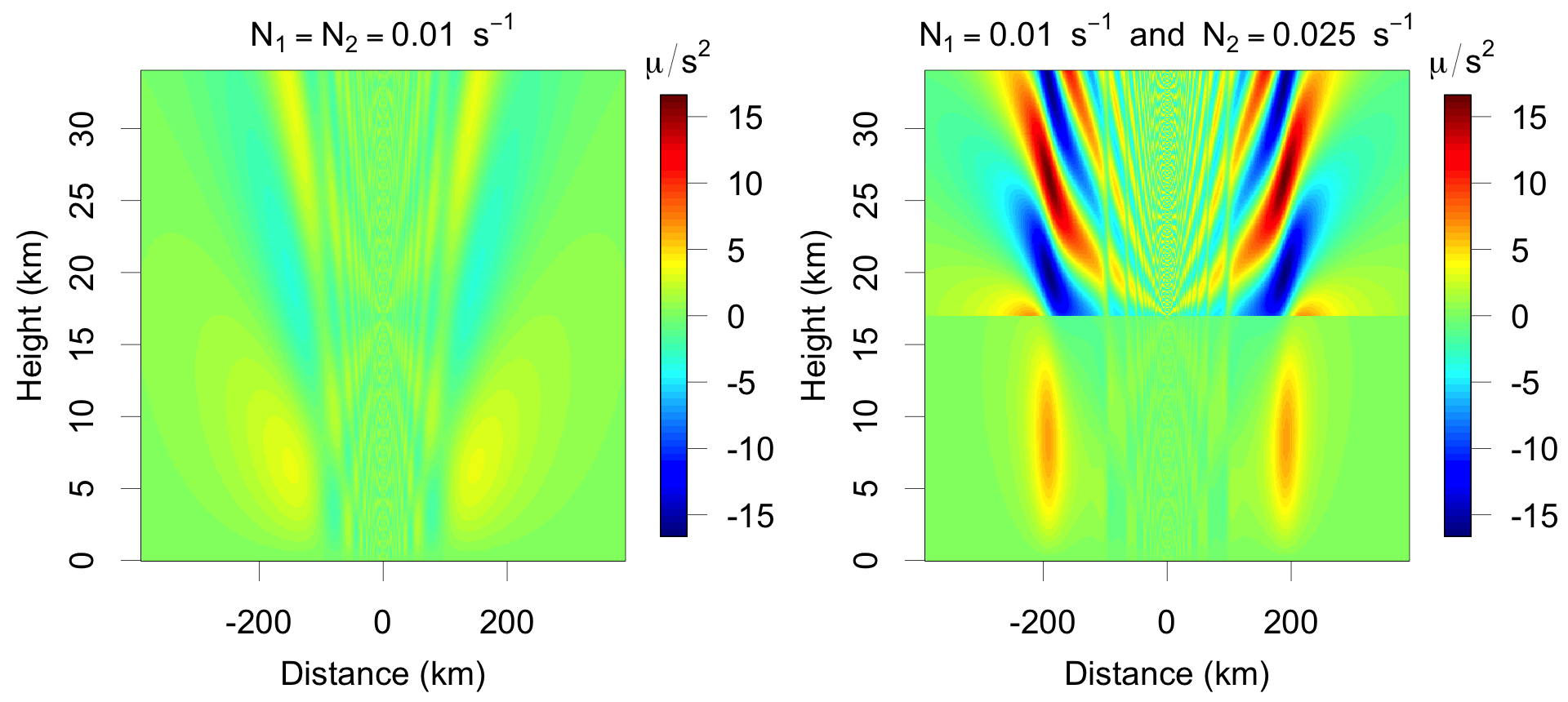
What happens when a storm heats the troposphere in a 2D atmosphere? A simple model of the resulting buoyancy can be found by assuming that the tropopause is a rigid lid. In that model, the buoyancy splits into two pulses that travel forever outward from the location of the heating. What is unrealistic about this picture is that those pulses never dissipate: they travel unaltered forever. This artificial behavior is a consequence of assuming a rigid lid at the tropopause.
In a more realistic atmosphere, the tropopause is not a rigid lid, but instead marks a transition between the stratification of the troposphere and the higher stratification of the stratosphere. In this paper, we derive the first Green's function for buoyancy in such an atmosphere. The resulting solutions show how the pulses melt away in time.
The buoyancy one hour after a first-baroclinic heating is applied to the troposphere at x=0 in a 2D Boussinesq fluid with (left) no change in stratification at 15 km and (right) a 2.5-fold increase in stratification at 15 km.