Romps, Reply to comments on MSE minus CAPE is the true conserved variable for an adiabatically lifted parcel, JAS, 2016

Paper

PDF

BibTeX

DOI

Description

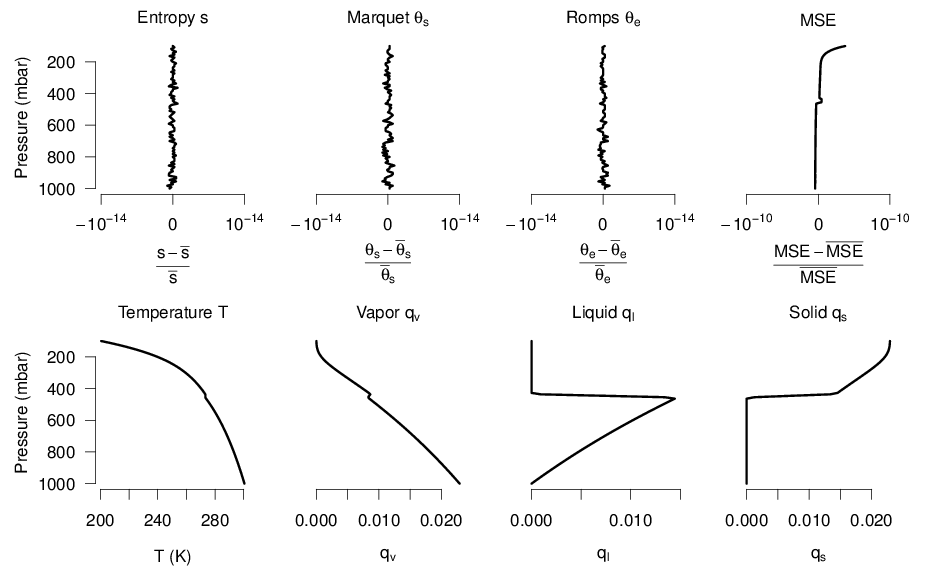
The MSE-CAPE paper elicited a comment from Pascal Marquet that contains an array of conceptual and numerical errors, and no substance relevant to the conservation MSE-CAPE for an adiabatically lifted parcel. In the original version of the comment submitted to JAS (available on the arXiv here), Marquet's primary claim was that I had used an expression for equivalent potential temperature that is not conserved for adiabatic ascent, whereas his expression for equivalent potential temperature is conserved. He then presented numerical results to back up this claim. As shown in this reply, that claim is false and his numerical results were caused by numerical error. If calculated correctly, as shown in the figure below, both expressions are conserved to within numerical rounding error.

After Marquet received a draft of my reply, he acknowledged the fallacy of his main point and apologized to the editor. At that point, the comment should have been rejected or withdrawn, but, instead, JAS accepted a revised comment from Marquet that contains a new set of strange and erroneous claims. One of those is the claim that I have fundamentally erred by identifying MSE-CAPE as the conserved variable rather than MSE+CAPE. This is false. This and the many other claims in Marquet's comment are addressed and corrected here. This reply also contains a discussion of the freedoms we have to choose additive energy and entropy constants when writing down the governing equations for moist air. Contrary to the claim by Marquet, we do not need to define the entropy such that it goes to zero at zero Kelvin. Instead, we can choose the energy and entropy of dry air and liquid water to be zero at the triple point, as is common practice. A thermodynamic system with two incompressible liquid phases is presented as a pedagogical example to illustrate this point.